
Germination Stage 4: Keep media on the drier side and lower media temperature to 60-62☏ (15-17☌), light levels can be increased to 3000-4000 f.c. with shading in hot weather Fertilize every other watering with 100-150ppm N (nitrate form) from 15-5-15, 17-5-17, or 13-2-13 keep media pH at 5.5-5.8 and EC at 1.0-1.5mmhos.
Germination Stage 3: Allow media to dry further between irrigations, practice a good wet/dry cycle but avoid wilting, media temperature should be 65-68☏ (18-20☌), light levels should be aroundģ000 f.c. Germination Stage 2: Dry down covering slightly to improve rooting and control floppiness, maintain media temperature at 65-70☏ (18-21☌), once cotyledons have opened light levels should be Keep medium uniformly moist, media temperature should be 65-70☏ (18-21☌), Keep light levels <1500 f.c.
FREEFALL FORMULA CODE
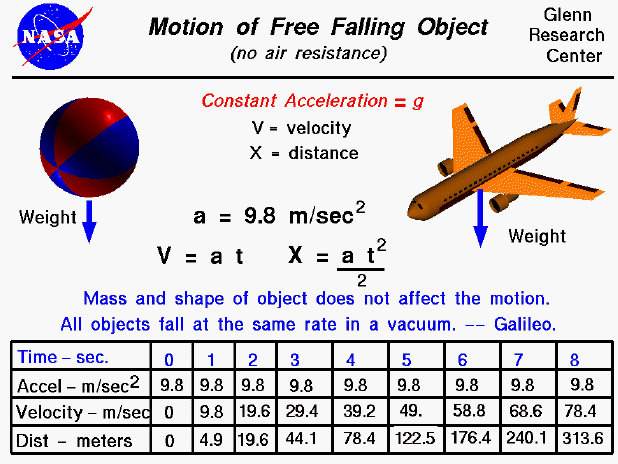
The only data to be stored was to relaunch the code in case of failure.Sowing/Media: Use a well-drained, disease-free, peat based plug medium with pH 5.5-5.8, ECĠ.75mmhos. In early days, when the internal and external memories were scarce all the computations, even the analysis, were made in the fly. If you keep going up in scale you must define another time, the interval between saves to disk. For example you keep one pair coord, velocity for ever 200 steps, the others 199 pairs are simply discarded after use. The standard procedure is to set number of steps to discard. But at some point you have a lot of "similar data", you need a smaller dt to get less error, but you don't need so many points to understand the solution. Second, the method (including others related) work better with a smaller dt. First, this work in this case because you are with a really tiny toy model, one particle in one dimension, but the same method could be used in 3 dimensions with a lot of particles with constrains or similar methods for pde where you have a lot of points to track, and the space will become a concern. I'm against storing all the dynamics in memory for two reasons. I never used np, so i can be missing something, but your code looks like you are programming python like it were Fortran. We know that function, it's v = a * t, we can write v = a*dt + v Gravity don't depend in y (at least near the earth surface), so v = fcn(t) Py.axhline(0.0, color='k', linestyle=':')įirst of all: can you work the euler method using only pencil and paper? Py.plot(t_array,Y,'-o', label="Analytic Method") Py.plot(t_array, V, 'x', label="Euler Method with res=") Print("Thus, Velocity and Position is",V,Y) #print('at time t = '.format(t_array,y_array)) #print("t_array:",t_array) # See what it looks like T_array = np.linspace(tmin, tmax, res, endpoint=False) # NOTE ENDPOINT HEREĭt = t_array - t_array # This is an easy way to define dt I also tried doing it this way, but am getting some weird results: This, however, gets me nowhere near the answer and I don't know where to input my differential equations for freefall. G=9.8 #freefall so acceleration is just gravity How would I go about doing this? I know that I have to set up arrays for both v and y and that I have to define Euler's method, but I am having issues doing that.

I am supposed to solve for v and y at the same time, though.

The equations are dv/dt=-g-(beta)t and dy/dt=v, where t is between 0 and 8.

I am trying to use Euler's method to solve and discretize some equations for freefall.


 0 kommentar(er)
0 kommentar(er)
